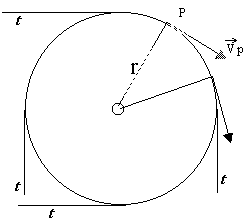
fig.1
Leggendo osserva attentamente le figure
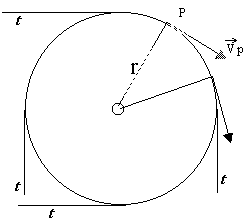
fig.1 |
Accelerazione Centripeta
Leggendo osserva attentamente le figure |
Nel Moto Circolare Uniforme (M.C.U.) il punto P viaggia di moto uniforme
(Vp=K) sulla circonferenza di raggio r [fig.1].
Pur essendo il moto definito uniforme esiste una accelerazione; la cosa � un poco
strana; la parola uniforme indica che si tratta di un moto a velocit� periferica costante,
per cui se la velocit� � sempre la stessa non dovrebbe esserci accelerazione.
Si deve pertanto accertare se tutte tre le caratteristiche del vettore sono costanti oppure no.
Si scopre cos� che la direzione (tangente t) del vettore Velocit� Periferica cambia mentre il
punto si sposta sulla traiettoria circolare [fig.1].
fig.a) i due vettori velocit� sono concorrenti e possono essere disegnati con un punto P
comune come in fig.b)
Se l'angolo a � sufficientemente piccolo, possiamo ipotizzare, osservando la figura 2 b)
che la lunghezza dell'arco MN di raggio V1 pu� ritenersi
praticamente uguale alla sua corda, (AB) che rappresenta l'intensit� del vettore
|V2 - V1|.
Dunque a � lo spazio angolare percorso dal punto che gira su se stesso w � la sua velocit�
angolare e Dt � l'infinitesimo intervallo di tempo necessario a compiere la rotazione a,
allora la tradizionale formula
Infatti l'accelerazione � per definizione variazione di velocit�, allora cosa causa l'
accelerazione?
Dobbiamo ricordare la definizione di vettore
Come otteniamo la formula
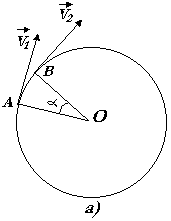
fig.2
Accellerazione Centripeta
Leggendo osserva attentamente le figure
fig.a) l'angolo a tra i due raggi � uguale a quello tra i due vettori velocit� fig.b) perch�
angoli compresi tra rette mutuamente perpendicolari
Il raggio di una circonferenza � sempre perpendicolare alla retta tangente passante per il
punto di intersezione della circonferenza con il raggio stesso.
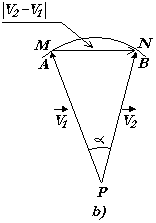
fig.2
Poich� la lunghezza di un arco � data dal prodotto del raggio per l'angolo al centro
corrispondente possiamo scrivere:
per la 1) sar�: (propriet� transitiva)
ac = |V2 - V1|/Dt = w � V1�Dt/Dt = w � V1
ricordando che
ac = w � V1 = w � w � R = w� � R c.v.d.
e
ac = w � V1 = V1/R � V1 = V1�/R c.v.d.
 |
9.2.2002 |
L'insegnante F.G.
